Research
We carry out experimental and theoretical research in a range of topics such as optical coherence, quantum entanglement, spontaneous parametric down-conversion, orbital angular momentum, squeezed states, vacuum fluctuations, and foundations of quantum theory. Our work lies at the intersection of quantum optics, nonlinear optics, coherence theory, and quantum information science.
Introduction: In the last few decades, numerous experiments have demonstrated that quantum systems can potentially outperform their classical counterparts in a variety of tasks such as computation [2, 3], secure communication [4–6], metrology [7, 8], and sensing [9]. Such enhanced capabilities are believed to primarily arise from two factors: (i) the intrinsic correlations of high-dimensional superposition states that enable parallelism in information processing, and (ii) the nonlocal correlations present in multiparticle quantum states that cannot be separated into states for their individual constituent particles. While the former intrinsic correlations, which enable physical systems to superpose and exhibit interference effects, constitute a property known as coherence that is found in both classical and quantum systems, the latter nonlocal correlations arise from a property known as entanglement, which is unique to quantum systems and has no known classical analog. In addition to enabling quantum-enhanced practical applications, entanglement also raises intriguing fundamental questions about the consistency and completeness of the quantum description of physical reality [10,11]. Our research focuses on theoretically characterizing the correlations of light fields and developing experimental methods for generating light fields with specifically tailored correlations and also measuring them in an efficient and accurate manner.

High-dimensional states of light and partially coherent fields: In contrast with the two-dimensional polarization degree of freedom, the orbital angular momentum (OAM) degree of freedom of light [12, 13] provides a discrete and infinite-dimensional basis for realizing high-dimensional states of light that have a number of distinct advantages such as improved security and enhanced bandwidth in optical communication protocols [14, 15], efficient gate implementations in computing protocols [16,17], and improved noise tolerance for fundamental tests of quantum theory [18, 19]. Moreover, when such high-dimensional superpositions are prepared in a partially coherent manner, they gain important advantages for applications such as long-distance communication and imaging through scattering media [20]. This is mainly because partially coherent fields are structurally more robust [21, 22], produce lesser scintillation [23], and also generate lesser speckle [24] under scattering and turbulence than their fully coherent counterparts. Our research aims to develop methods for generating high-dimensional states and partially coherent light fields with desired coherence properties in a controlled way, but also to innovate techniques for measuring such fields in an efficient and accurate manner.
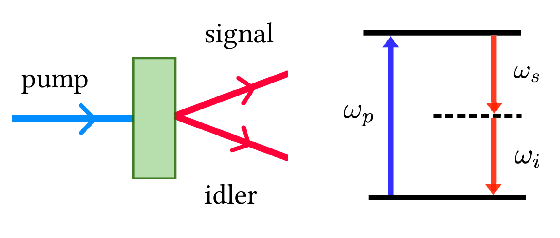
Nonclassical light from spontaneous parametric down-conversion (SPDC): SPDC is a nonlinear optical process in which a single photon from an incident field known as pump interacts with a nonlinear crystal to produce a pair of entangled photons known as signal and idler [25]. This process is routinely harnessed for producing entangled states and squeezed states in fundamental quantum optics experiments [26, 27] and optical quantum technologies [28, 29]. Furthermore, by pumping two crystals in series or parallel configuration, researchers have realized nonlinear interferometers [30] and induced coherence experiments [31] that not only have important applications in phase metrology [32] and imaging [33], but have also led to major insights on indistinguishability and its role in interference [34]. Our research will work towards controlled generation of entangled states from PDC using a variety of means such as tailoring the coherence of the pump, tuning the parameters of nonlinear interferometers, and also employing partially coherent seed fields. In addition, we will work towards developing novel interferometric and mode projection-based techniques to measure such states in an accurate and efficient manner. Furthermore, we will also work towards scaling up these entangled states to span higher number of dimensions and include more than two photons with the two-fold aim of probing the fundamental physics of high-dimensional multipartite entanglement and investigating novel ways in which such entanglement can be harnessed for more powerful information processing capabilities.
References:
- Mandel, L. & Wolf, E., “Optical coherence and quantum optics”, Cambridge University Press (1995).
- Shor, P. W. , “Algorithms for quantum computation: Discrete logarithms and factoring” , Foundations of Computer Science, 1994 Proceedings, 35th Annual Symposium on (1994), 124–134.
- Arute, F. et al. “Quantum supremacy using a programmable superconducting processor”, Nature 574, 505–510 (2019).
- Bennett, C. H. & Brassard, G. Advances in Cryptology: Proceedings of Crypto84, August 1984 (1984).
- Ekert, A. K. “Quantum cryptography based on Bells theorem”, Phys. Rev. Lett. 67, 661–663 (1991).
- Pirandola, S. et al. “Advances in quantum cryptography”, Advances in optics and photonics 12, 1012–1236 (2020).
- Caves, C. M., “Quantum-mechanical noise in an interferometer”, Phys. Rev. D 23, 1693–1708 (1981).
- Giovannetti, V., Lloyd, S. & Maccone, L. “Quantum-Enhanced Measurements Beating the Standard Quantum Limit”, Science 306, 1330–1336 (2004).
- Degen, C. L., Reinhard, F. & Cappellaro, P., “Quantum sensing”, Reviews of Modern Physics 89, 035002 (2017).
- Einstein, A., Podolsky, B. & Rosen, N., “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Phys. Rev. 47, 777–780 (1935).
- Bell, J. S., “On the Einstein Podolsky Rosen paradox”, Physics 1, 195 (1964).
- Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. “Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes”, Phys. Rev. A 45, 8185–8189 (1992).
- Erhard, M., Fickler, R., Krenn, M. & Zeilinger, A., “Twisted photons: new quantum perspectives in high dimensions”, Light: Science & Applications 7, 17146 (2018).
- Karimipour, V., Bahraminasab, A. & Bagherinezhad, S., “Quantum key distribution for d-level systems with generalized Bell states”, Phys. Rev. A 65, 052331 (2002).
- Fujiwara, M., Takeoka, M., Mizuno, J. & Sasaki, M. “Exceeding the Classical Capacity Limit in a Quantum Optical Channel”, Phys. Rev. Lett. 90, 167906 (2003).
- Wang, J. et al. “Terabit free-space data transmission employing orbital angular momentum multiplexing”, Nature Photonics 6, 488–496 (2012).
- Bozinovic, N. et al. “Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers”, Science 340, 1545–1548 (2013).
- Kaszlikowski, D., Gnaciński, P., Żukowski, M., Miklaszewski, W. & Zeilinger, A. “Violations of Local Realism by Two Entangled N-Dimensional Systems Are Stronger than for Two Qubits”, Phys. Rev. Lett. 85, 4418–4421 (21 Nov. 2000).
- Collins, D., Gisin, N., Linden, N., Massar, S. & Popescu, S. “Bell Inequalities for Arbitrarily High-Dimensional Systems”, Phys. Rev. Lett. 88, 040404 (2002).
- Gbur, G. & Visser, T. Progress in optics 285–341 (Elsevier, 2010).
- Roychowdhury, H. & Wolf, E. “Invariance of spectrum of light generated by a class of quasi-homogenous sources on propagation through turbulence”, Optics Communications 241, 11–15 (2004).
- Bhattacharjee, A. & Jha, A. K. “Experimental demonstration of structural robustness of spatially partially coherent fields in turbulence”, Optics Letters 45, 4068–4071 (2020).
- Fante, R. L., “The effect of source temporal coherence on light scintillations in weak turbulence”, JOSA 69, 71–73 (1979).
- Kim, J. et al. “Optical coherence tomography speckle reduction by a partially spatially coherent source”, Journal of Biomedical Optics 10, 064034 (2005).
- Boyd, R. W. “Nonlinear optics” (Academic press, 2020).
- Hong, C. K., Ou, Z. Y. & Mandel, L. ,”Measurement of subpicosecond time intervals between two photons by interference”, Phys. Rev. Lett. 59, 2044–2046 (1987).
- Shalm, L. K. et al. “Strong loophole-free test of local realism”, Physical Review Letters 115, 250402 (2015).
- Bouwmeester, D. et al. “Experimental quantum teleportation”, Nature 390, 575–579 (1997).
- Jennewein, T., Simon, C., Weihs, G., Weinfurter, H. & Zeilinger, A. “Quantum Cryptography with Entangled Photons”, Phys. Rev. Lett. 84, 4729–4732 (2000).
- Chekhova, M. V. & Ou, Z. Y. “Nonlinear interferometers in quantum optics”, Adv. Opt. Photon. 8, 104–155 (2016).
- Wang, L. J., Zou, X. Y. & Mandel, L., “Induced coherence without induced emission”, Phys. Rev. A 44, 4614–4622 (1991).
- Yurke, B., McCall, S. L. & Klauder, J. R., “SU(2) and SU(1,1) interferometers”, Phys. Rev. A 33, 4033–4054 (1986).
- Lemos, G. B. et al. “Quantum imaging with undetected photons”, Nature 512, 409–412 (2014).
- Zou, X. Y., Wang, L. J. & Mandel, L., “Induced coherence and indistinguishability in optical interference”, Phys. Rev. Lett. 67, 318–321 (1991).